k - 최근접 이웃(K-Nearest Neighbor, KNN)
k-nearest neighbor 알고리즘은 단순히 게으른 것을 말하는 것이 아닌
알고리즘의 훈련 데이터에서 판별 함수(discriminative function)를 학습하는 것이 아닌
훈련 데이터를 메모리에 저장해서 이용한다.
( 비모수 모델, 인스턴스 기반 모델-훈련 데이터셋을 메모리에 저장하는 것이 특징이다.
게으른 학습은 인스턴스 기반 학습의 특별한 경우이며 학습 과정에서 비용이 전혀 들지 않음)
KNN algorithm process
1) 숫자 k와 거리 측정 기준을 선택
2) 분류하려는 샘플에서 k개의 최근접 이웃을 찾는다.
3) 다수결 투표를 통해 클래스 레이블을 할당
선택한 거리 측정 기준에 따라 KNN알고리즘이 훈련 데이터셋에서 분류하려는 포인트와 가장 가까운
샘플 k개를 찾는다. 새로운 데이터 포인트의 클래스 레이블은 이 k개의 최근접 이웃에서 다수결 투표를 하여
결정된다.
이와 같은 메모리 기반 방식의 분류기는 수집된 새로운 훈련 데이터를 즉시 적응할 수 있다는 것이 주요 장점이다.
하지만 새로운 샘플을 분류하는 계산 복잡도가 단점이다.
데이터셋의 차원(특성)이 적고 알고리즘이 k-d같은 효율적인 데이터 구조로 구현되어 있지 않으면,
최악의 경우 훈련 데이터셋의 샘플 개수는 선형적으로 증가한다.
또한 훈련 단계가 없기 때문에 훈련 데이터를 버릴 수 없다. 대규모 데이터셋에서 작업한다면,
저장 공간에 문제가 생긴다.
유클리안 거리 측정기를 이용한 사이킷런의 KNN 모델
from sklearn.neighbors import KNeighborsClassifier
knn=KNeighborsClassifier(n_neighbors=5, p=2, metric='minkowski')
knn.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined, classifier=knn, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [stadardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
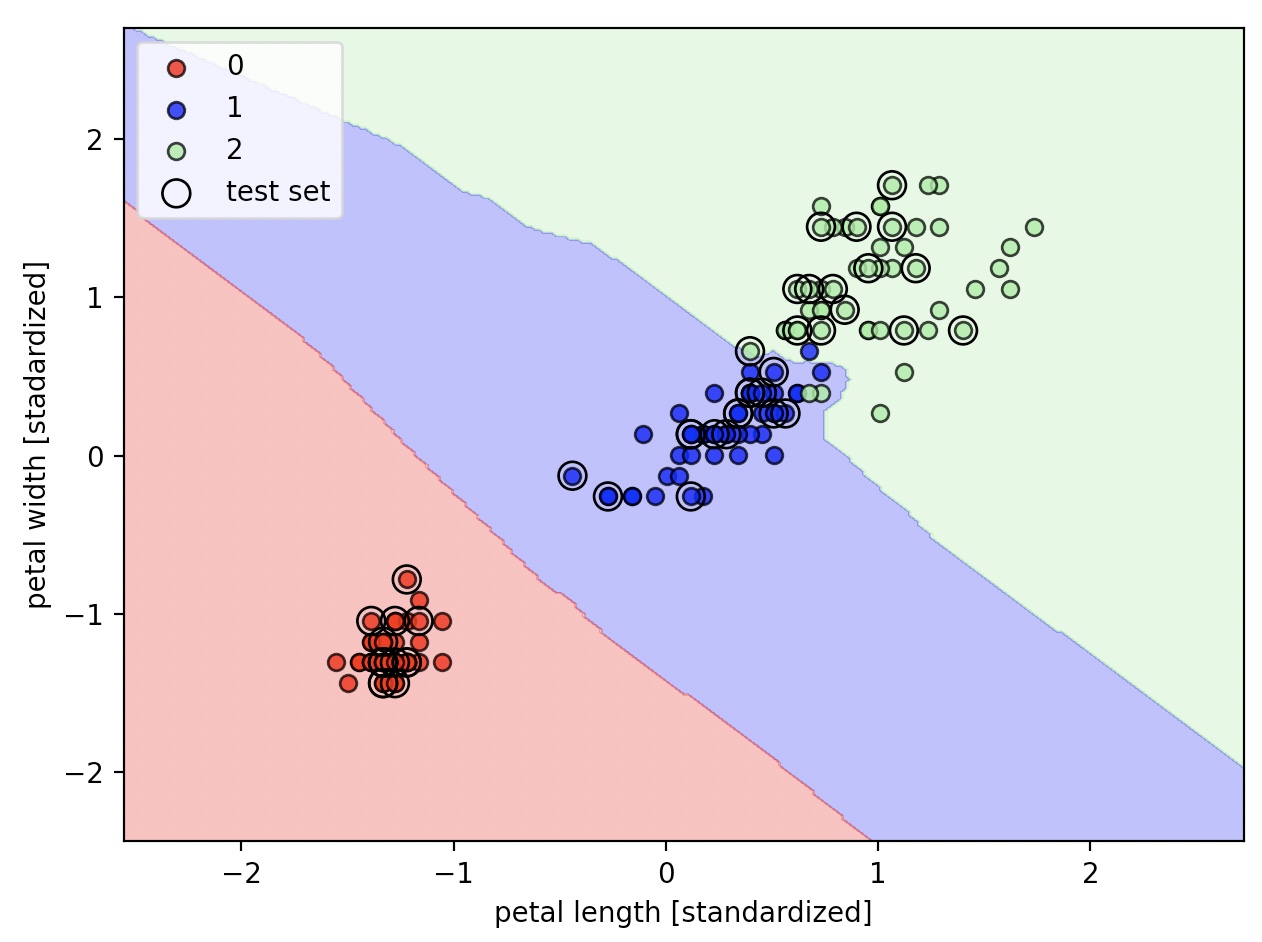
KNeighborsClassifier 클래스의 metric 매개변수의 기본값은 ‘minkowski’이고 p의 기본값은 2이다.
minkowski는 유클리디안 거리와 맨헤튼(Manhattan) 거리를 일반화한 것이다.
p=2이면 유클리디안 거리가 되고, p=1이면 맨헤튼 거리가 된다.
동점처리
다수결 투표가 동일한 경우, 사이킷런의 KNN 구현은 분류하려는 데이터 포인트에 더 가까운 이웃을 예측으로 선택한다.
이웃의 거리가 같다면, 훈련 데이터셋에서 먼저 나타난 샘플의 클래스 레이블을 선택
차원의 저주(Curse of dimensionality)
KNN은 차원의 저주로 과대적합되기 쉽다.
고정된 크기의 훈련 데이터셋이 차원인 늘어남에 따라 특성 공간이 점점 희소해지는 현상이다.
고차원 공간에서는 가장 가까운 이웃이라도, 좋은 추정값을 만들기에는 너무 멀리 떨어져 있음
선형 회귀에서는 과대적합을 피하기 위해서 규제를 적용하였다.
결정트리나 KNN 처럼 규제를 적용할 수 없는 모델에서는 특성 선택과 차원 축소 기법을 이용하면,
차원의 저주를 피하는데 도움이 된다.